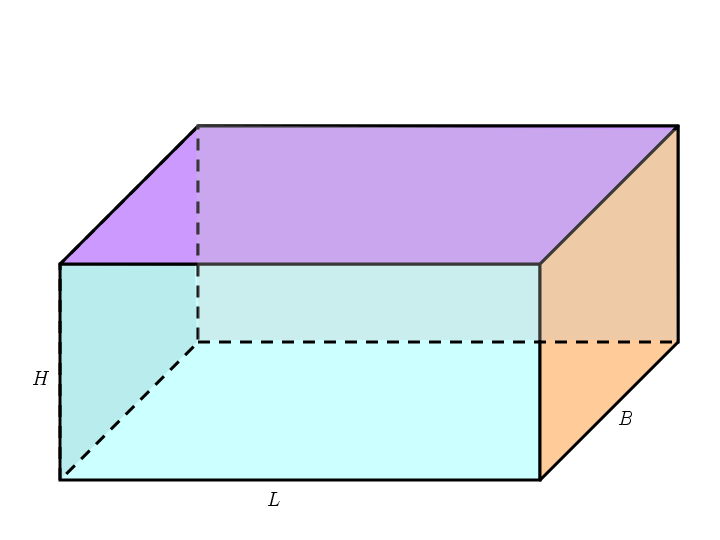
Rumus Luas Permukaan Balok – Bentuk balok sudah pasti tidak asing lagi buat kalian. Ini dikarenakan dalam pelajaran matematika yang membahas bangun ruang, balok adalah salah satu bentuk yang pertama kali diperkenalkan, mulai dari cara menggambarnya hingga berbagai rumus-rumusnya. Ada rumus volume dan juga rumus luas permukaan balok.
Artikel kali ini ini kami secara khusus akan membahas rumus luas permukaan balok dan juga melihat berbagai contoh-contoh soalnya. Namun sebelum itu, mari kita mengenal balok secara lebih dekat.
Balok adalah sebuah bangun ruang yang terbentuk dari tiga pasang persegi panjang. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Balok yang memiliki sisi enam persegi yang sama dan sebangun disebut sebagai kubus. Balok memiliki beberapa istilah untuk sisinya, seperti panjang, lebar dan tinggi.
Daftar Isi
Pengertian Balok

Balok adalah bangun ruang tiga dimensi yang dibentuk oleh dua pasang persegi dan empat pasang persegi panjang, dengan paling tidak satu pasang di antaranya berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Balok yang dibentuk oleh enam persegi sama dan sebangun disebut sebagai kubus.
Adanya sejumlah rusuk di bangun ruang tersebut menjadi pembeda dari bentuk lainnya. Selain itu, balok adalah bangun ruang yang memiliki panjang dan lebar sisi berbeda. Perbedaan balok dan kubus adalah jumlah rusuknya. Balok memiliki rusuk lebih panjang.
Secara rinci, elemen-elemen balok antara lain:
- Panjang adalah rusuk terpanjang dari alas balok.
- Lebar adalah rusuk terpendek dari sisi alas balok.
- Tinggi adalah rusuk yang tegak lurus terhadap panjang dan lebar balok.
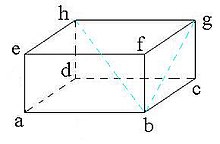
Berdasarkan gambar balok di atas, kita bisa melihat tiga pasang sisi yang letaknya saling berhadapan memiliki bentuk dan ukuran yang sama, antara lain:
- Sisi ABCD = sisi EFGH
- Sisi ABFE = sisi DCGH
- Sisi ADHE = sisi BCGF
Oleh karena itu, bisa kita simpulkan jika gambar tersebut ialah sebuah balok, yaitu terdapat tiga pasang sisi yang ukurannya sama besar dan letaknya saling berhadapan, serta berbentuk persegi panjang. Jadi, jika dirincikan bisa juga dikatakan bahwa pengertian atau definisi balok adalah sebagai berikut.
- Memiliki tiga pasang sisi yang yang letaknya saling berhadapan.
- Memiliki tiga pasang sisi yang ukuran masing-masing pasangannya sama besar.
- Memiliki minimal dua pasang sisi yang berbentuk persegi panjang.
Contoh balok yang bisa kita temukan di sekitar kita dalam kehidupan sehari-hari antara lain:
- Lemari.
- Kardus.
- Akuarium.
- Balok kayu.
- Lemari es.
- Radio.
- Tempat tisu.
- Tempat pensil.
- Kotak P3K.
- Kado
- Novel atau buku tebal.
- Salon atau speaker.
- Penghapus.
- Batu bata.
- Bak mandi.
- Toples kotak.
- Music box.
- Kamera saku.
- Kotak brankas.
- Kotak korek api.
- Kotak tok jajanan.
- Koper.
Rumus-rumus balok antara lain:
1. Panjang Diagonal Ruang
2. Panjang Diagonal Ruang Seluruhnya
3. Panjang Diagonal Bidang
4. Panjang Diagonal Bidang Seluruhnya
5. Luas Bidang Diagonal
6. Luas Bidang Diagonal Seluruhnya
Ciri-Ciri Bangun Ruang Balok
Balok merupakan salah satu bangun ruang yang hampir sama dengan kubus, tetapi balok mempunyai rusuk yang lebih panjang. Nah, berikut adalah ciri-ciri balok!
1. Memiliki 6 Buah Sisi
Sisi pada sebuah balok menjadi bidang yang membatasi antara balok dengan tiga pasang sisi yang memiliki bentuk dan ukuran yang sama, jika saling berhadapan. Sebuah balok pasti memiliki 6 buah sisi yang berbentuk persegi atau persegi panjang. Sisi tersebut berada di samping kiri dan kanan, atas dan bawah, serta depan dan belakang.
Berdasarkan contoh gambar balok di atas, 6 sisi tersebut adalah:
- Sisi samping kiri dan sisi samping kanan = ADHE = BCGF.
- Sisi alas (bawah) dan sisi atas = ABCD = EFGH.
- Sisi depan dan sisi belakang = ABFE = DCGH.
2. Memiliki 12 Rusuk
Rusuk adalah garis yang memotong antara dua sisi bidang pada balok. Rusuk pada balok ini pastilah sejajar dan mempunyai panjang yang sama. Jika kamu perhatikan, rusuk itu seperti kerangka penyusun balok. Sebuah balok memiliki 12 buah rusuk, terdiri atas 4 rusuk panjang, 4 rusuk lebar, dan 4 rusuk tinggi. Jika kamu memperhatikan contoh gambar balok sebelumnya, maka 12 rusuk tersebut adalah:
- 4 rusuk panjang = AB = DC = EF = HG.
- 4 rusuk lebar = AD = BC = EH = FG.
- 4 rusuk tinggi = AE = BF = CG = DH.
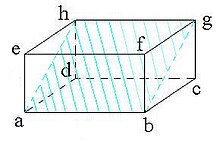
3. Memiliki 12 Diagonal Bidang
Diagonal bidang dapat disebut juga dengan diagonal sisi, yakni ruas garis yang menghubungan antara dua titik sudut yang berhadapan pada setiap bidang atau sisi dari balok. Sebelumnya, telah dijelaskan bahwa balok itu memiliki 6 buah sisi, maka dari itu diagonal bidangnya berjumlah 12. Jika kamu memperhatikan contoh gambar balok, maka 12 diagonal bidang tersebut adalah:
- Diagonal AC = EG.
- Diagonal BD = FH.
- Diagonal AH = BG.
- Diagonal CF = DE.
- Diagonal AF = DG.
- Diagonal BE = CH.
4. Memiliki 8 Titik Sudut
Titik sudut pada setiap balok adalah 8 buah. Titik-titik sudut tersebut terbentuk oleh adanya pertemuan dari setiap 3 rusuk balok. Jika kamu memperhatikan contoh gambar balok sebelumnya, maka 8 titik sudut tersebut adalah titik A, B, C, D, E, F, G, dan H.
5. Memiliki 4 Diagonal Ruang
Diagonal ruang merupakan garis yang menghubungkan antara dua buah titik sudut yang saling berhadapan pada satu ruang. Jika kamu memperhatikan kembali contoh gambar balok, maka 4 diagonal ruang tersebut adalah:
- Ruas garis AG.
- Ruas garis HB.
- Ruas garis DF.
- Ruas garis CE
6. Memiliki 6 Bidang Diagonal
Bidang diagonal berbeda dengan diagonal bidang yang sebelumnya telah diuraikan sebelumnya. Bidang diagonal adalah bidang yang dibatasi oleh dua rusuk dan dua diagonal bidang. Nah, pada sebuah balok, terdapat 6 bidang diagonal.
Jika kamu memperhatikan contoh gambar balok, 6 bidang diagonal tersebut adalah:
- Bidang diagonal ACGE = BDHF.
- Bidang diagonal ABGH = DCFE
- Bidang diagonal BCHE = ADGF.
7. Memiliki Luas Permukaan dan Volume
Sama halnya dengan bangun ruang lainnya, balok juga memiliki luas permukaan dan volume. Volume berkaitan dengan seberapa luas ruangan yang terdapat di dalam suatu bangun ruang. Untuk menentukan luas permukaan dan volume pada balok, dapat ditemukan dengan menggunakan rumus tertentu. Rumus untuk menghitung luas permukaan pada balok adalah:
Keterangan:
p = panjang balok
l = lebar balok
t = tinggi balok
Sementara itu, untuk menentukan volume yang terdapat pada sebuah balok, juga memiliki rumus tertentu, yakni:
Keterangan:
p = panjang balok
l = lebar balok
t = tinggi balok
Rumus Luas Permukaan Balok
Setiap sisi dari balok memiliki bentuk persegi panjang. Rumus yang biasanya kita gunakan untuk menentukan luas persegi panjang adalah panjang x lebar. Lalu, untuk menghitung luas permukaan dari balok apakah kita harus menjumlahkan setiap luas dari sisi balok yang berbentuk persegi panjang ini? Ini agak rumit karena ada rumus yang lebih mudah untuk digunakan, yaitu:
Selain itu, ada pula rumus alternatif dari luas balok yang bisa diketahui:
- L = 2pl + 2lt + 2pt
- V = p x l x t
- P = V : (l x t)
Rumus luas permukaan balok tanpa tutup meliputi:
- L = pl + 2(lt) + 2(pt)
Keterangan:
L = luas permukaan
p = panjang
l = lebar
t = tinggi
Contoh Soal-Soal Balok
Untuk bisa lebih memahami rumus ini mari kita perhatikan contoh-contoh yang diberikan berikut ini.
Contoh soal 1:
Sebuah balok memiliki ukuran panjang 200 cm, lebar 2 cm dan tinggi 10 cm. Berapakah luas permukaan dari balok tersebut?
Jawab:
L = 2 x (p . l + p. t + l. t)
L = 2 x (200 x 2 + 200 x 10 + 2 x 10)
L = 2 x (400 + 2.000 + 20)
L = 2 x (2.420)
L = 4.840 cm2
Contoh soal 2:
Sebuah balok memiliki ukuran panjang 12 cm, lebar 7 cm, dan tinggi 5 cm. Berapakah luas permukaan dari balok tersebut?
Jawab:
L = 2 x (p . l + p. t + l. t)
L = 2 x (12 x 7 + 7 x 5 + 12 x 5)
L = 2 x (84 + 35 + 60)
L = 2 x (179)
L = 358 cm²
Contoh soal 3:
Sebuah balok memiliki ukuran panjang 12 cm, lebar 7 cm, dan tinggi 5 cm. Berapakah ukuran volume balok tersebut?
Jawab:
V = p x l x t
V = 12 x 7 x 5
V = 420 cm²
Contoh soal 4:
Diketahui bahwa terdapat panjang, lebar, dan tinggi suatu balok berturut-turut adalah 3 cm, 2 cm, 4 cm. Hitunglah volume balok tersebut?
Jawab:
V = p x l x t
V = 3 x 2 x 4
V = 24 cm3
Sahabat Grameds tidak perlu khawatir karena kalian dapat mempelajari lebih luas lagi tentang cara menghitung volume balok atau bangun ruang lainnya melalui rekomendasi buku pelajaran berikut ini. Cara menghitung volume balok dapat dipelajari di bangku sekolah dasar kelas 5. Kamu dapat mengetahuinya lebih dulu jika telah membaca dan melatihnya sehari-hari di rumah, sehingga mudah saat menemukan soal seperti ini dalam pelajaran di sekolah. Langsung saja klik produk buku di bawah ini!
Contoh Soal 5:
Diketahui suatu balok memiliki panjang 10 m, lebar 2 m, dan tinggi 200 cm. Hitunglah berapa volume balok tersebut?
Jawab:
Cara penyelesaian contoh soal yang kedua pada dasarnya sama saja dengan soal sebelumnya, tetapi tinggi balok tersebut belum menggunakan satuan yang sama. Oleh karena itu, kamu harus menyamakan satuan tersebut terlebih dahulu agar memiliki satuan yang sama.
Panjang = 10 m.
Lebar = 2 m.
Tinggi = 200 cm menjadi 2 m.
Selanjutnya, masukkan rumus V = p x l x t
V = 10 x 2 x 2
V = 40 m3
Contoh soal 6:
Sebuah balok mempunyai panjang 300 cm, lebar 10 cm, dan tinggi 20 cm. Hitunglah berapa volume balok tersebut?
Jawab:
V = p x l x t
V = 300 x 10 x 20
V = 60.000 cm3
Contoh soal 7:
Diketahui bahwa Budi memiliki sebuah kolam berbentuk balok dengan panjang 80 cm, lebar 60 cm, dan tingginya 40 cm. Kolam tersebut tentunya akan diisi oleh air. Berapa banyak air yang dibutuhkan untuk mengisi ⅔ kolam milik Budi tersebut?
Jawab:
Diketahui: panjang kolam (p) = 80 cm, lebar (l) = 60 cm, dan tinggi (t) = 40 cm.
Ditanya: volume balok di ⅔ kolam
V = ⅔ x p x l x t
V = ⅔ (80 cm x 60 cm x 40 cm)
V = ⅔ (192.000 cm3)
V = 128.000 cm3
Jadi, banyaknya air yang dibutuhkan untuk mengisi ⅔ kolam milik Budi adalah 128.000 cm3.
Contoh soal 8:
Jojo ingin membuat sebuah kolam lele berbentuk balok dengan lebar 40 cm, panjang 3/2 kali lebarnya, dan tinggi kolam lele 4 lebihnya dari ukuran lebar tersebut. Berapakah volume kolam lele yang akan dibutuhkan oleh Jojo?
Jawab:
Lebar kolam lele (l) = 40 cm
Panjang kolam lele (p) = 3/2 x (l) = 3/2 x 40 = 60 cm
Tinggi kolam lele (t) = (l) + 4 = 40 + 4 = 44 cm
Rumus: V = p x l x t
V = 60 cm x 40 cm x 44 cm
V = 105.600 cm3
Jadi, volume pada kolam lele yang dibutuhkan Jojo adalah 105.600 cm3.
Grameds juga bisa membaca salah satu buku berikut ini yang berjudul Matematika Dasar yang ditulis oleh Afidah Khairunnisa, yang berisikan tentang informasi peran perkembangan ilmu pengetahuan dan teknologi serta referensi dan acuan bagi mahasiswa atau peminat matematika dalam mempelajari salah satu bangun ruang atau ilmu matematika yang lain. Dapatkan bukunya dengan mengklik di bawah ini ya Grameds!
Contoh soal 9:
Diketahui sebuah balok memiliki ukuran panjang 10 cm, lebar 6 cm, tinggi 5 cm. Hitunglah luas permukaan balok tersebut!
Jawab:
L = 2 x (p × l + p × t + l × t)
L = 2 x (10 × 6 + 10 × 5 + 6 × 5)
L = 2 x (60 + 50 + 30)
L = 2 x 140
L = 280 cm²
Jadi, luas permukaan balok tersebut adalah 280 cm².
Contoh soal 10:
Sebuah balok mempunyai panjang 20 cm, lebar 10 cm, dan tinggi 5 cm. Hitunglah luas permukaan balok tersebut!
Jawab:
L = 2 x (p × l + p × t + l × t)
L = 2 x (20 × 10 + 20 × 5 + 10 × 5)
L = 2 x (200 + 100 + 50)
L = 2 x 350
L = 700 cm²
Jadi, luas permukaan balok tersebut adalah 700 cm².
Contoh soal 11:
Berapakah luas permukaan balok yang memiliki panjang 12 cm, lebar 7 cm, dan tinggi 8 cm?
Jawab:
L = 2 × (pl + lt + pt)
L = 2 x (12 x 7 + 12 x 8 + 7 x 8)
L = 2 x (84 + 96 + 54)
L = 2 x 236
L = 472 cm²
Jadi, luas permukaan balok tersebut adalah 472 cm².
Contoh soal 12:
Lebar dan tinggi sebuah balok berturut-turut adalah 3 cm dan 2 cm. Jika luas permukaannya 62 cm², berapakah panjang balok tersebut?
Jawab:
L = 2 × (pl + pt + lt)
62 = 2 ×(3p + 2p + [2×3])
62/2 = 3p + 2p + 6
31 – 6 = 5p
25 = 5p
p = 5
Jadi, panjang balok tersebut adalah 5 cm.
Contoh soal 13:
Diketahui volume sebuah balok adalah 1.000 cm³. Jika lebar balok 10 cm dan tingginya adalah 5 cm, berapa luas permukaan balok?
Jawab:
P = V : (l x t)
P = 1.000 : (10 x 5)
P = 1.000 : 50
P = 20 cm
L = 2 x (pl + pt + lt)
L = 2 x (20.10 + 20.5 + 10.5)
L = 2 x (200 + 100 + 50)
L = 2 x 350
L = 700 cm²
Jadi, luas permukaan balok adalah 700 cm² jika diketahui volumenya 1.000 cm³.
Contoh soal 14:
Volume balok adalah 300 cm³. Jika panjang balok 10 cm dan lebarnya 6 cm, tentukan luas permukaan balok!
Jawab:
t = V : (p x l)
t = 300 : (10 x 6)
t = 300 : 60
t = 5 cm
L = 2 x (pl + pt + lt)
L = 2 x (10.6 + 10.5 + 6.5)
L = 2 x (60 + 50 + 30)
L = 2 x 140
L = 280 cm²
Jadi, luas permukaan balok adalah 280 cm² jika diketahui volumenya 300 cm³.
Contoh soal 15:
Berapakah luas permukaan balok tanpa tutup yang mempunyai panjang 20 cm, lebar 6 cm, dan tinggi 11 cm?
Jawab:
L = pl + 2(lt) + 2(pt)
L = (20.6) + 2(6.11) + 2(20.11)
L = 120 + 132 + 440
L = 692 cm²
Jadi, luas permukaan balok tanpa tutup adalah 692 cm².
Contoh soal 16:
Sebuah balok mempunyai ukuran panjang 10 cm, lebar 5 cm, dan tinggi 2 cm. Hitunglah luas permukaan balok tersebut!
Nah, itu dia sedikit contoh singkat yang bisa membantu kamu lebih memahami rumus luas permukaan balok. Penjelasan mengenai bangun ruang balok dan rumus menghitung luas permukaannya beserta contoh soalnya, dapat membantu para siswa yang sedang belajar matematika atau sebagai bahan untuk membantu siswa-siswi belajar.
BACA JUGA: