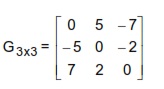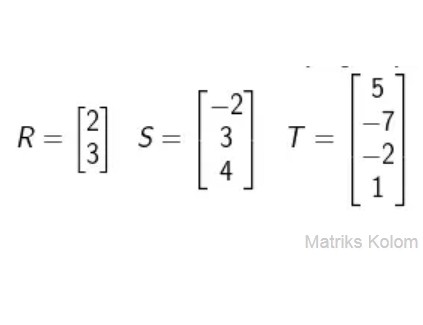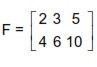Matriks menjadi salah satu cara yang paling mudah untuk menyelesaikan persoalan matematis yang memiliki banyak variabel. Biasanya ia diaplikasikan pada bidang matematika, ekonomi, dan teknik.
Matriks sendiri memiliki banyak jenis. Salah satunya matriks identitas yang mana diagonalnya berupa angka satu. Lalu, bagaimana cara mengoperasikannya. Berikut akan dijelaskan lebih rinci mengenai matriks identitas.
Daftar Isi
Sekilas Tentang Matriks
Matriks merupakan susunan bilangan, simbol, atau ekspresi yang disusun dalam kolom dan baris sehingga membentuk suatu bangun segi empat. Sebagai gambaran awal matriks, Grameds dapat menyimak contoh matriks berukuran 2 x 3 di bawah ini.

Ukuran matriks ditentukan berdasarkan jumlah baris dan kolom yang dimilikinya. Matriks dengan m kolom dan n baris disebut dengan matriks m x n, yang mana m dan n disebut dengan dimensinya. Misalnya matriks di atas disebut dengan matriks 2 x 3. Hal tersebut disebabkan, matriks tersebut terdiri dari 2 baris dan 3 kolom.
Matriks dengan jumlah baris dan kolom yang sama disebut dengan matriks persegi. Adapun matriks dengan jumlah satu baris disebut dengan vektor baris. Sedangkan, matriks dengan satu kolom disebut dengan vektor kolom.
Adapun matriks tak terbatas merupakan matriks dengan jumlah baris atau kolom yang tak terbatas (atau keduanya). Pada beberapa konteks matriks yang dipertimbangkan tanpa baris atau tanpa kolom disebut dengan matriks kosong.
Untuk penjelasan lebih lanjut, Grameds dapat menyimak gambar di bawah ini.

Baris m adalah horizontal dan kolom n adalah vertikal. Setiap elemen matriks sering kali dilambangkan dengan variabel dua notasei indeks. Misalnya, a2,1 mewakili elemen pada baris kedua dan kolom pertama dari matriks A.
Setiap objek dalam matriks A berdimensi m x n sering dilambangja dengan ai,j. Yang mana dilai maksimum i = m dan nilai maksimum j = n. Objek dalam matriks disebut dengan elemen, entri atau anggota matriks.
Jika dua matriks memiliki dimensi yang sama (masing-masing matriks memiliki jumlah baris dan jumlah kolom yang sama) maka kedua matriks tersebut dapat dilakukan penjumlahan atau pengurangan secara elemen demi elemen. Namun, berdasarkan aturan perkalian matriks, syarat perkalian matriks, yakni ketika jumlah kolom matriks pertama sama dengan jumlah baris matriks kedua pada perkalian dua matriks.
Maksudnya, perkalian matriks m x n dengan matriks n x p menghasilkan matriks m x p. Oleh sebab itu, perkalian matriks tidak bersifat komutatif. Pada umumnya, matriks digunakan untuk merepresentasikan transformasi linear, yakni suati generalisasi fungsi linear seperti f (x) = 4x.
Misalnya, efek rotasi pada ruang dimensi tiga merupakan sebuah transformasi linear yang dilambangkan dengan matriks R. Jika v adalah sebuah vektor di dimensi tiga, hasil Rv menyatakan posisi titik tersebut setelah dirotasi.
Matriks dapat diterapkan dalam berbagai bidang sians. Misalnya pada fisika berupa mekanika klasik, optika, dan mekanika kuantum. Matriks juga digunakan untuk mempelajari keadaan fisis, seperti pergerakan planet. Pada bidang computer graphics, matriks diterapkan untuk memanipulasi model 3D dan memproyeksikannya ke sebuah layar dua dimensi.
Pada bidang teori probabilitas dan statistika, matriks digunakan sebagai penjelas probabilitas keadaan. Seperti pada algoritma pagerank dalam menentukan urutan halaman pencairan di Google. Adapun kalkulus matriks menggeneralisasi bentuk analitik klasik dari tutunan dan eksponensial ke dimensi yang lebih tinggi. Matriks juga diterapkan dalam bidang ekonomi untuk menjelaskan sistem ekonomi relasi.
Fungsi Matriks dalam Kehidupan Sehari-hari
Meskipun operasi matriks terlihat sulit, tetapi ia memiliki banyak manfaat untuk mempermudah pekerjaan-pekerjaan manusia dalam kehidupan sehari-hari. Berikut beberapa manfaat mempelajari matriks dalam kehidupan sehari-hari.
- Membantu pekerjaan insinyur dalam menyelesaikan masalah-masalah dengan banyak variabel.
- Matriks juga dapat digunakan untuk membuat rapor dan jurnal.
- Menyelesaikan suatu sistem persamaan linier, transformasi geometri, menentukan jadwal siaran televisi, dan pemrogaman komputer.
- Membantu menganalisis permasalahan ekonomi yang memiliki berbagai macam variabel.
- Sebagai cara untuk menganalisis dalam bidang statistik, pendidikan, sains, ekonomi, dan teknologi.
- Membantu mencari solusi pada operasi penyelidikan, misalnya operasi penyelidikan sumber daya alam (batu bara, minyak bumi, dan sebagainya).
Konsep dan Sifat Matriks Identitas
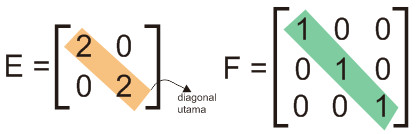
Matriks identitas merupakan matriks yang memiliki nilai pada elemen diagonal utama berupa satu dan elemen di luar diagonal utama bernilai nol. Matriks identitas memiliki sifat sama seperti bilangan 1. Yang mana ketika sebuah matriks dikalikan dengan matriks identitas maka hasilnya tidak akan berubah.
Matriks identitas dilambangkan dengan In atau sekadar I jika ukuran n dapat diketahui dari konteks pembahasan. Beberapa buku menggunakan singkatan U dan E berdasarkan dengan “unit matrix” yang dalam bahasa Indonesia berarti matriks satuan. Adapun terjemahannya dalam bahasa Jerman, yakni “einheitsmatrix”.
Agar Grameds lebih memahami matriks identitas maka dapat menyimak contoh di bawah ini.
Contoh Soal dan Pembahasan Matriks
Untuk lebih memahami matriks identitas, Grameds dapat menyimak beberapa contoh soal matriks identitas dan penyelesaiannya.
1. Jika diketahui matriks A dan B seperti berikut ini.

Tentukan apakah AB = A dan BA = A.
Jawab:

Jadi, terbukti jika AB = BA = A maka matriks B merupakan matriks identitas I.
2. Buktikan jika AI3 = A = I3A pada matriks-matriks berikut ini.

Jawab:

Jadi, AI3 = A = I3A terbukti benar.
3. Jika diketahui matriks G dan A sebagai berikut. Maka, buktikan G + A = A + G = G

Jawab:

Jadi, G + A = A + G = G terbukti benar.
4. Jika diketahui matriks seperti di bawah ini.

Maka buktikan bahwa P + A = A + P = P.
Jawab:

Jadi, operasi matriks P + A = A + P = P terbukti benar.
5. Buktikan jika matriks AB = BA = A pada matriks A dan B berikut ini.

Jawab:

Jadi, AB = BA = A terbukti benar.
Jenis Matriks Berdasarkan Elemen Penyusunnya
Matriks memiliki beragam jenis. Berikut beberapa klasifikasi matriks berdasarkan elemen-elemen penyusunnya.
1. Matriks Nol
Matriks nol merupakan matriks yang seluruh elemen penyusunnya berupa angka nol. Berikut contoh matriks nol.
2. Matriks Diagonal
Matriks diagonal merupakan matriks yang seluruh elemen di luar diagonal utama berupa angka nol dan minimal ada satu elemen pada diagonal utama yang bukan angka nol. Berikut contoh matriks diagonal.
3. Matriks Skalar
Matriks skalar merupakan matriks yang seluruh elemennya berada di diagonal yang sama. Berikut contoh matriks skalar.
4. Matriks Simetri
Matriks simetri merupakan matriks persegi yang setiap elemennya selain elemen diagonal terdiri dari angka yang simetri terhadap diagonal utamanya. Berikut contoh matriks simetri.
5. Matriks Simetri Miring
Matriks simetri miring merupakan matriks simetri yang elemen-elemennya, selain elemen diagonalnya saling berlawanan. Berikut contoh matriks simetri miring.
6. Matriks Identitas
Matriks identitas merupakan matriks yang seluruh elemen diagonal utama bernilai satu dan elemen di luar utama bernilai nol. Berikut contoh matriks identitas.
7. Matriks Segitiga Atas
Matriks segitiga atas merupakan matriks diagonal yang memiliki elemen di bagian kanan (atas) diagonal utama bernilai tidak sama dengan nol. Berikut contoh matriks segitiga atas.
8. Matriks Segitiga Bawah
Matriks segitiga bawah merupakan matriks diagonal yang mana elemen di bagian sebelah kiri (bawah) diagonal utama bernilai tidak sama dengan nol. Berikut contoh matriks segitiga bawah.
9. Matriks Transpose
Matriks transpose merupakan matriks yang diperoleh dari pemindahan elemen-elemen baris menjadi elemen kolom atau sebaliknya. Berikut contoh transpose matriks.
Jenis Matriks Berdasarkan Ordo
Berikut klasifikasi matriks berdasarkan ordo menjadi beberapa kategori sebagai berikut.
1. Matriks Bujur Sangkar/Persegi
Matriks bujur sangkar.persegi merupakan matriks dengan ordo n x n atau banyaknya baris sama dengan jumlah kolom. Berikut contoh matriks bujur sangkar.
2. Matriks Baris
Matriks baris merupakan matriks yang memiliki ordo 1 x n atau hanya terdiri dari satu baris. Berikut contoh matriks baris.
3. Matriks Kolom
Matriks kolom merupakan matriks yang hanya terdiri dari satu kolom atau memiliki ordo n x 1. Berikut contoh matriks kolom.
4. Matriks Tegak
Matriks tegak merupakan matriks yang memiliki ordo m x n dengan m > n. berikut contoh matriks tegak.
5. Matriks Datar
Matriks datar merupakan matriks dengan ordo m x n dengan m < n. Berikut contoh matriks datar.
Klasifikasi Matriks Berdasarkan Sifat Operasi
Matriks diklasifikasikan berdasarka sifat operasinya menjadi dua kategori. Berikut rincian keduannya.
1. Matriks Singular (singular matriks)
Matriks singular merupakan matriks yang memiliki determinan bernilai no dan tidak memiliki invers. Berikut contoh dari matriks singular.
2. Matriks Non Singular (non singular matriks)
Matriks non singular merupakan matriks yang determinannya tidak sama dengan nol dan memiliki invers. Berikut contoh dari matriks non singular.

- Angka Penting
- Bangun Ruang
- Besaran Turunan
- Bilangan Bulat
- Bilangan Bulat Positif
- Cara Menghitung Akar Pangkat 3
- Ciri-Ciri Segitiga Sembarang
- Contoh Soal Matematika Kelas 4 Semester 2
- Deret Matematika
- Determinan Matriks
- Himpunan
- Konsep Penalaran Matematika
- Rumus Volume Limas
- Rumus Trapesium
- Limas
- Rumus Lingkaran
- Luas Belah Ketupat
- Rumus Tabung
- Rumus Segitiga
- Rumus Segitiga Sama Kaki
- Simetri Lipat dan Simetri Putar
- Ciri-ciri Balok
- Jenis Matriks
- Determinan Matriks
- Penjumlahan Matriks
- Persamaan Linear
- Matriks Singular
- Rumus ABC
- Rumus Matriks
- Rumus Bangun Ruang
- Rumus Peluang Kejadian
- Rumus Skala
- Rumus Varians: Pengertian, Cara Menghitung dan Contoh
- Satuan Panjang
- Sifat-Sifat Eksponen
- Sudut Siku-Siku
- Matriks Identitas
- Limit Fungsi Trigonometri
- Transpose Matriks
- Turunan Fungsi Aljabar
- Rumus Volume Tabung
- Bangun Ruang Kubus: Rumus Keliling Dan Contoh Penerapannya
- Persamaan Lingkaran
- Penemu Angka Nol
- Cara Mengubah Pecahan Biasa Menjadi Desimal
- Sifat Bangun Datar
- Cara Menghitung Volume Balok
- Gerbang Logika
- Integer
- Jenis-jenis Sudut
- Rumus Lingkaran
- Rumus Luas Permukaan Limas
- Rumus Mean, Median, dan Modus
- Rumus Satuan Deviasi
- Rumus Peluang
- Pengertian Determinan
- Pengertian Trigonometri
- Rumus Keliling Segitiga Sembarang
- Rumus Trapesium Sembarang
- Skala
- Satuan Berat
- Daftar Angka Romawi
- Materi Persamaan Kuadrat
- Modus: Rumus dan Perbedaannya
- Soal Matematika Kelas 4
- Unsur Lingkaran dan Rumusnya