Pengertian Invers Matriks – Hai Grameds! Apa kabar kalian semuanya? Semoga masih dalam keadaan sehat dan tidak galau ya karena materi matematika yang satu ini. Tidak heran juga jika kalian mampir ke sini untuk belajar lebih jauh tentang invers matriks, iya kan?
Mendengar istilah invers matriks, kalian mungkin akan mengaitkannya dengan materi fungsi invers. Namun, kedua hal ini berbeda. Invers adalah kebalikan atau lawan dari sesuatu, sedangkan fungsi invers merupakan suatu fungsi matematika yang berkebalikan dengan fungsi asalnya. Lantas, apa itu invers matriks?
Dalam modul Matematika Umum Kelas XI yang disusun oleh Yusdi Irfan (2020), invers matriks adalah matriks baru yang merupakan kebalikan dari matriks asal. Matriks adalah susunan dengan bentuk persegi panjang atau persegi yang tersusun dari angka dan diatur dalam baris maupun kolom.
Invers matriks adalah salah satu metode penting untuk menyelesaikan soal-soal di dalam sebuah matriks. Sebelum mencari invers suatu matriks harus menentukan determinannya terlebih dahulu. Determinan merupakan nilai yang dapat dihitung dari unsur-unsur suatu matriks persegi.
Invers sendiri dapat diartikan sebagai lawan dari sesuatu (kebalikan). Jika suatu matriks memiliki invers, dapat dikatakan matriks tersebut adalah matriks nonsingular. Sebaliknya, jika suatu matriks tidak memiliki invers, maka matriks tersebut merupakan matriks singular.
Invers matriks adalah sebuah kebalikan (invers) dari kedua matriks. Apabila matriks tersebut dikalikan akan menghasilkan matriks persegi (AB = BA = |). Simbol dari invers matriks adalah pangkat -1 dan terletak di atas hurufnya. Sebagai contoh, matriks B adalah invers matriks A sehingga ditulis B = A–1 dan matriks A adalah invers dari matriks B ditulis A = B-1. Matriks A dan B merupakan dua matriks yang saling invers (berkebalikan). Invers matriks terdiri dari dua jenis, yaitu matriks persegi (2×2) dan matriks 3×3.
Bagaimana rumusannya? Soal seperti apa yang dapat diselesaikan dalam bentuk matriks? Untuk menjawab pertanyaan tersebut, Gramedia akan mengulasnya dengan memberikan contoh-contoh soal beserta pembahasannya. Mari simak bersama-sama.
Daftar Isi
Pengertian Invers Matriks
Perlu diingat, baris merupakan susunan horizontal, sedangkan kolom susunan vertikal. Jika digambarkan dalam model matematika, berikut penjelasannya.
Berikut ini merupakan tabel dan matriks dari kandungan makanan.
|
Kandungan Makanan |
Jenis Makanan (Setiap Ons) |
||
| K | L | M | |
| Kalsium | 30 | 10 | 30 |
| Besi | 10 | 10 | 10 |
| Vitamin | 10 | 30 | 20 |

Dari gambar dan tabel di atas, kalian dapat melihat jenis tabel kandungan makanan yang terdiri atas variabel (kalsium, besi, dan vitamin), serta jenis makanan (setiap ons-nya). Tabel kandungan tersebut diubah ke dalam bentuk sebuah matriks agar lebih memudahkan perhitungan variabel tersebut.
Pada gambar di atas, terlihat matriks terdiri atas 3 baris dan 3 kolom, sehingga matriks KLM disebut matriks 3 x 3. Oleh sebab itu, matriks adalah susunan bilangan-bilangan berbentuk persegi panjang atau persegi yang tersusun dalam baris dan kolom yang terletak di dalam kurung atau siku. Bilangan dalam kurung dinamakan elemen, unsur, atau komponen matriks. Pada matriks KLM di atas, elemen matriksnya adalah sebagai berikut K={30, 10, 10}, L={10, 10, 30}, dan M={30, 10, 20}.
Sebuah matriks mempunyai sebuah ordo (m x n) misalnya Am x n (A2 x 3), maka ordo dari matriks A adalah 2 x 3. Dimana 2 adalah baris dan 3 adalah kolom. Apabila sebuah matriks ordonya m = n, maka matriks itu dinamakan matriks persegi, sedangkan jika m ≠ n disebut matriks persegi panjang.
Dalam aljabar linear, sebuah matriks persegi berukuran terbalikkan (invertible) atau tidak singular, jika terdapat matriks persegi dengan ukuran yang sama dengan , dan memenuhi hubungan:
dengan melambangkan matriks identitas berukuran , dan perkalian yang dilakukan merupakan perkalian matriks yang umum. Jika hubungan tersebut berlaku, maka matriks disebut sebagai balikan atau invers (multiplikatif) dari matriks , dan diberi lambang .
Matriks persegi tidak dapat dibalik disebut dengan matriks singular. Matriks persegi bersifat singular jika dan hanya jika nilai determinannya 0. Matriks yang bukan matriks persegi (berukuran dan ) tidak memiliki invers. Namun dalam beberapa kasus, matriks tersebut mungkin memiliki invers kiri atau invers kanan. Jika matriks berukuran dengan rank (nilai ), maka memiliki invers kiri.
Invers kiri ini adalah sebuah matriks berukuran yang memenuhi hubungan Adapun jika rank matriks adalah (nilai ), maka memiliki invers kanan; yakni sebuah matriks berukuran yang memenuhi hubungan
Konsep dan Rumus Invers Matriks
Invers matriks A adalah suatu matriks baru yang berkebalikan dengan matriks A dengan notasi A-1. Jika matriks tersebut dikalikan dengan invers matriksnya, maka akan terbentuk matriks identitas. Umumnya, penggunaan matriks ini untuk memecahkan sistem persamaan linier (SPL). Untuk menyelesaikan invers matriks, terdapat beberapa aturan berdasarkan ordo matriks yaitu 2 x 2 dan 3 x 3.
Berikut rumus invers matriks:

Invers matriks 2 x 2 bisa diperoleh langsung caranya dengan menukar elemen pada diagonal utama, berikan tanda negatif pada elemen lain, kemudian bagi setiap elemen matriks dengan determinan. Sementara itu, invers matriks ordo 3 x 3 diperoleh dengan dua cara, yaitu adjoin dan transformasi baris elementer.
Rumus pada gambar di atas merupakan rumus invers matriks 3 x 3 dengan cara adjoin. Kita juga dapat mencari invers pada matriks dengan menentukan determinannya terlebih dahulu. Determinan adalah nilai yang dihitung dari unsur-unsur suatu matriks persegi.
1. Rumus Invers Matriks Persegi Berordo 2×2
Berikut rumus invers matriks yang digunakan untuk matriks berordo 2×2 seperti dikutip dari Cepat Tuntas Kuasai Matematika karangan HJ Sriyanto (2009:100).

Invers matriks berordo 2 dapat langsung diperoleh dengan cara:
- Tukar elemen-elemen pada diagonal utamanya.
- Berikan tanda negatif pada elemen-elemen lainnya.
- Bagilah setiap elemen matriks dengan determinannya.
2. Rumus Invers Matriks Berordo 3×3
Mencari invers matriks berordo 3×3 dapat dilakukan dengan dua cara, yaitu dengan adjoin dan transformasi baris elementer. Adjoin matriks merupakan transpose dari suatu matriks yang elemen-elemennya merupakan kofaktor dari elemen-elemen matriks tersebut. Lalu, rumus invers matriks berordo 3×3 menjadi:
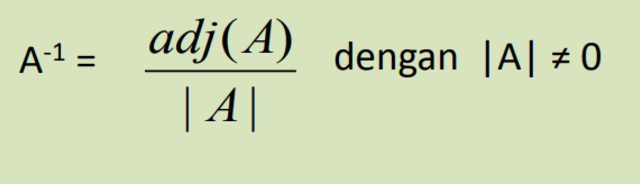
Dalam menentukan invers matriks An dengan cara transformasi baris elementer bisa menggunakan langkah-langkah berikut ini:
- Bentuk matriks ini (An|ln), dengan lm merupakan matriks identitas berordo n.
- Transformasikan matriks (An|ln) ke dalam bentuk (ln|Bn) dengan transformasi elemen baris.
- Hasil dari langkah 2, didapat invers dari matriks An yaitu Bn.
Notasi yang sering digunakan dalam transformasi baris elementer di antaranya:
- Bi ↔ Bj: Menukarkan elemen-elemen baris ke-I dengan elemen-elemen baris ke-j.
- Bi: mengalihkan setiap elemen-elemen baris ke-I dengan skalar k.
- Bi + kBj: jumlah elemen-elemen pada baris ke-I dengan k kali elemen-elemen garis ke-j.
Sifat-Sifat Invers Matriks
Misal matriks A berordo n x n dengan n ∈ N, dan determinan A tidak sama dengan nol, jika A-1 adalah invers dari A maka (A-1)-1 = A
Misal matriks A dan B berordo n x n dengan n ∈ N dan determinan A dan B tidak sama dengan nol, jika A -1 dan B-1 adalah invers dari matriks A dan B maka (AB)-1= B-1 A-1
Contoh Soal Invers Matriks
 1. Teorema Matriks Terbalikkan
1. Teorema Matriks Terbalikkan
Sifat keterbalikkan sebuah matriks berhubungan erat dengan banyak sifat lain yang dimiliki matriks tersebut. Misalkan adalah matriks persegi berukuran , dengan entri-entri adalah elemen dari suatu lapangan (misalnya, lapangan bilangan real ). Semua pernyataan berikut ekuivalen, dalam artian antara matriks memenuhi semua pernyataan, atau matriks tidak memenuhi satupun pernyataan yang ada.
- Matriks terbalikkan. Dengan kata lain, matriks memiliki sebuah invers (atau tidak singular).
- Ada sebuah matriks berukuran yang memenuhi
- Matriks dapat diubah menjadi matriks identitas lewat serangkaian operasi baris elementer, atau lewat serangkaian operasi kolom elementer.
- Matriks dapat dinyatakan sebagai perkalian (dengan jumlah terhingga) matriks-matriks elementer.
- Matriks memiliki posisi pivot. Posisi pivot adalah nilai 1 pertama sebuah baris pada matriks bentuk eselon baris tereduksi (reduced row echelon form).
- Persamaan hanya memiliki solusi trivial, yakni .
- Persamaan tepat memiliki satu solusi, untuk semua .
- Transformasi linear adalah sebuah bijeksi dari ke .
- Kernel dari trivial; dengan kata lain hanya mengandung vektor nol sebagai elemennya, sehingga
- Determinan dari sama dengan 0.
- Bilangan 0 bukan nilai eigen dari matriks .
- Rank penuh; dengan kata lain, .
- Kolom-kolom dari saling bebas linear. Ini mengartikan tidak mungkin menyatakan sebuah kolom matriks sebagai kombinasi penjumlahan kolom-kolom yang lain.
- Span dari kolom-kolom matriks adalah . Artinya, himpunan semua kombinasi linear dari kolom-kolom akan sama dengan .
- Ruang kolom dari matriks adalah . Ruang kolom adalah ruang vektor yang dibentuk oleh kolom-kolom matriks .
- Kolom-kolom matriks membentuk sebuah basis bagi .
- Transpos dari , yakni matriks juga terbalikkan. Hal ini mengartikan baris-baris dari matriks juga memenuhi sifat-sifat yang sama dengan kolom-kolom matriks.
- Matriks memiliki invers kiri (yakni matriks sehingga ) dan invers kanan (yakni matriks sehingga ). Lebih lanjut, nilai kedua invers tersebut sama, .
2. Hubungan dengan Adjugat
Adjugat dari suatu matriks dapat digunakan untuk mencari invers dari , dengan menggunakan hubungan:
Jika memiliki invers, maka
3. Sifat-Sifat Lain
Selain sifat-sifat pada bagian-bagian sebelumnya, matriks berukuran yang terbalikkan juga memiliki beberapa sifat berikut:
- ;
- untuk sembarang skalar yang tidak sama dengan 0;
- ;
- ;
- Untuk sembarang matriks yang dapat dibalik dan yang berukuran sama dengan , akan berlaku . Hal ini dapat diperumum untuk kasus matriks-matriks berukuran dan dapat dibalik, yang akan memiliki hubungan
- Jika memiliki kolom-kolom yang saling ortonormal, maka ; dengan menyatakan invers Moore–Penrose dan adalah vektor.
Istilah-Istilah dalam Invers Matriks
Ada istilah-istilah yang sering dikenal dalam materi matriks, yaitu matriks persegi, matriks baris, matriks kolom, matriks nol, matriks diagonal, matriks identitas, matriks skalar, tranpos matriks, dan invers matriks. Simak di bawah ya penjelasannya!
1. Matriks Persegi
Matriks persegi adalah matriks yang jumlah elemen pada baris dan kolom adalah sama. Selain itu, karena bentuknya berupa bujur sangkar, terdapat diagonal utama dan diagonal sekunder pada matriks persegi. Diagonal utama adalah bagian diagonal yang menurun ke bawah contohnya adalah {a11, a22, a33, ………., amn}. Sedangkan diagonal sekunder adalah bagian diagonal yang naik ke atas contohnya adalah {am1, a1n, dan lain-lain}.
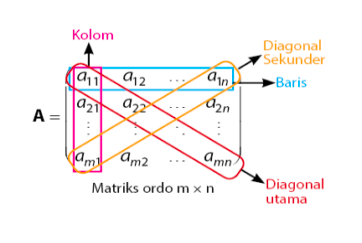

2. Matriks Baris
Matriks baris adalah suatu matriks yang hanya mempunyai 1 baris saja, sehingga ordo dari tersebut adalah A1xn . Contoh dari matriks baris tersebut adalah:
A = [ 2 0 ] dan B = [ 3 -1 5 0 ].
Matriks A adalah matriks baris berordo 1 x 2. Sedangkan matriks B adalah matriks baris berordo 1 x 4.
3. Matriks Kolom
Matriks kolom adalah suatu matriks yang hanya mempunyai 1 kolom saja. Matriks kolom adalah matriks yang berordo m x 1. Contoh matriks kolom adalah sebagai berikut:

Matriks A adalah matriks kolom berordo 3 x 1. Sedangkan matriks B adalah matriks kolom berordo 4 x 1.
4. Matriks Nol
Matriks nol adalah matriks yang semua elemennya adalah bilangan nol. Matriks nol dinotasikan sebagai 0mxn . Contoh matriks nol adalah sebagai berikut:

5. Matriks Identitas
Matriks identitas atau sering disebut matriks satuan adalah matriks yang semua diagonalnya adalah sama yaitu bernilai 1. Simbol dari matriks identitas adalah | miring ( | ). Contoh dari matriks identitas adalah sebagai berikut:

6. Matriks Skalar
Matriks skalar adalah matriks yang elemen-elemen diagonalnya bernilai sama. Sehingga a11= a22= ………= amn = k. Nilai k dapat bernilai sembarang. Contoh dari matriks skalar adalah sebagai berikut:
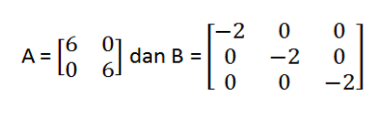
Matriks A adalah matriks skalar berordo 2. Sedangkan matriks B adalah matriks skalar berordo 3.
7. Transpos Matriks
Transpos matriks adalah matriks baru yang diperoleh dengan dengan menukarkan letak baris dan kolom dari matriks sebelumnya. Transpos matriks disimbolkan dengan memberi aksen atau T di bagian atas pada matriks sebelumnya. Contoh A menjadi A’, B menjadi BT. Rumusan transpos matriks adalah sebagai berikut:
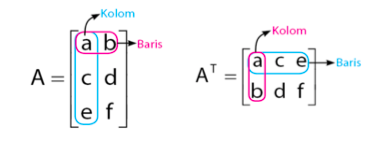
Contoh dari transpos matriks adalah sebagai berikut:

8. Invers Matriks
Invers matriks adalah sebuah kebalikan (invers) dari kedua matriks di mana apabila matriks tersebut dikalikan menghasilkan matriks persegi (AB = BA = |). Simbol dari invers matriks adalah pangkat -1 di atas hurufnya. Contoh matriks B adalah invers matriks A ditulis B = A–1 dan matriks A adalah invers dari matriks B ditulis A = B-1. Matriks A dan B merupakan dua matriks yang saling invers (berkebalikan). Invers matriks terdiri dari dua jenis yaitu matriks persegi (2×2) dan matriks 3×3.
Invers matriks A berordo 2 dapat langsung kita peroleh dengan cara:
- Tukar elemen-elemen pada diagonal utamanya.
- Berikan tanda negatif pada elemen-elemen lainnya.
- Bagilah setiap elemen matriks dengan determinannya.
Rumusan dari invers matriks persegi berordo 2 adalah sebagai berikut:
Jika matriks A = [ a b c d ] dengan determinan A = a.d – b.c, maka invers matriks A dirumuskan sebagai berikut:

Dalam penyelesaian matriks 3 x 3, ada beberapa istilah yang harus kita ketahui yaitu determinan sarrus, minor, kofaktor, dan adjoin. Sebagai contoh apabila terdapat matriks 3 x 3 sebagai berikut: A = [ a b c d e f g h i ]maka rumus untuk mencari inversnya adalah sebagai berikut:

Dari persamaan diatas, ada det (A) yaitu determinan A dan Adj (A) yaitu adjoin A, di mana rumus untuk mencari determinan A menggunakan rumus determinan sarrus yaitu sebagai berikut:
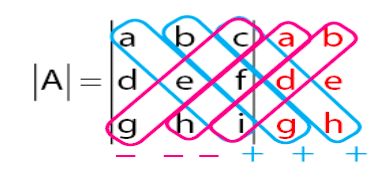
Nilai determinanya sarrusnya menjadi = a x e x | + b x f x g – c x d x h – c x e x g – a x f x h – b x d x |. Selanjutnya penentuan Adjoin A dapat terlihat dari gambar dibawah ini.
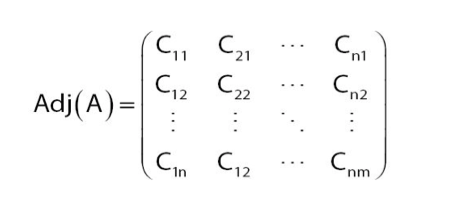
Dari gambar terlihat terdapat simbol C kapital, di mana letak nilai C sudah ditranspos dari baris ke kolom. C merupakan singkatan dari kofaktor. Penentuan nilai kofaktor diperoleh dari penentuan nilai minor suatu matriks. Penentuan nilai kofaktor dan minor adalah sebagai berikut:

Bagaimana Grameds dengan rumus-rumus di atas? Tidak perlu bingung, cobain saja dulu contoh soal dari kami tentang invers matriks 2 x 2 dan invers matriks 3 x 3.
Contoh Soal 1:
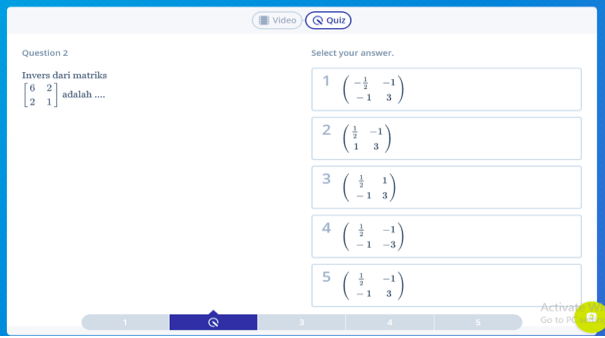
Pembahasan:

Contoh Soal 2:
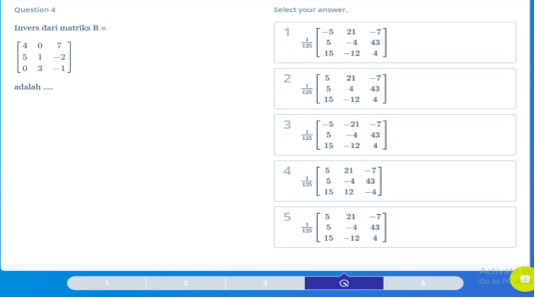
Pembahasan:

Rekomendasi Buku & Artikel Terkait
- Angka Penting
- Bangun Ruang
- Besaran Turunan
- Bilangan Bulat
- Bilangan Bulat Positif
- Cara Menghitung Akar Pangkat 3
- Ciri-Ciri Segitiga Sembarang
- Contoh Soal Matematika Kelas 4 Semester 2
- Deret Matematika
- Determinan Matriks
- Himpunan
- Konsep Penalaran Matematika
- Rumus Volume Limas
- Rumus Trapesium
- Limas
- Rumus Lingkaran
- Luas Belah Ketupat
- Rumus Tabung
- Rumus Segitiga
- Rumus Segitiga Sama Kaki
- Simetri Lipat dan Simetri Putar
- Ciri-ciri Balok
- Jenis Matriks
- Determinan Matriks
- Penjumlahan Matriks
- Persamaan Linear
- Matriks Singular
- Rumus ABC
- Rumus Matriks
- Rumus Bangun Ruang
- Rumus Peluang Kejadian
- Rumus Skala
- Rumus Varians: Pengertian, Cara Menghitung dan Contoh
- Satuan Panjang
- Sifat-Sifat Eksponen
- Sudut Siku-Siku
- Matriks Identitas
- Limit Fungsi Trigonometri
- Transpose Matriks
- Turunan Fungsi Aljabar
- Rumus Volume Tabung
- Bangun Ruang Kubus: Rumus Keliling Dan Contoh Penerapannya
- Persamaan Lingkaran
- Penemu Angka Nol
- Cara Mengubah Pecahan Biasa Menjadi Desimal
- Sifat Bangun Datar
- Cara Menghitung Volume Balok
- Gerbang Logika
- Integer
- Jenis-jenis Sudut
- Rumus Lingkaran
- Rumus Luas Permukaan Limas
- Rumus Mean, Median, dan Modus
- Rumus Satuan Deviasi
- Rumus Peluang
- Pengertian Determinan
- Pengertian Trigonometri
- Rumus Keliling Segitiga Sembarang
- Rumus Trapesium Sembarang
- Skala
- Satuan Berat
- Daftar Angka Romawi
- Materi Persamaan Kuadrat
- Modus: Rumus dan Perbedaannya
- Soal Matematika Kelas 4
- Unsur Lingkaran dan Rumusnya























 .
.
 .
.


 .
.



 .
.


















